Серія QR

P = Допуск паралельності поворотного стола 0,1 мм

R = Допуск круглості поворотного стола 0,1 мм

C = Допуск циліндричності поворотного стола 0,1 мм

M = Момент/крутний момент

L = Відстань від вісі обертання до крайньої точки

D = Відхилення від горизонталі

QR07                                                    При L = 100 мм

D = Відхилення від горизонталі

F = Зусилля

D = Відхилення від горизонталі

F = Зусилля

D = Відхилення від горизонталі

F = Зусилля

D = Відхилення від горизонталі

F = Зусилля

D = Відхилення від горизонталі

F = Зусилля

Mres = Крутний момент

P = Тиск

Максимально допустиме навантаження

МОМЕНТ ПРИКЛАДЕНИХ СИЛ:

- МОМЕНТ СТАТИЧНИХ СИЛ (T_s)

Статична сила циліндра – сила, що виробляється навантаженням при відсутності переміщень. Наприклад, вага об'єкту при негоризонтальному розташуванні площини обертання

F = вага переміщуваних мас (Н)

L = плече між центром мас і віссю обертання

T_s = момент, створюваний силою тяжіння (Н∙м)

α = кут відхилення вісі обертання об'єкту від вертикальної вісі

ЦИЛІНДР РОЗТАШОВАНИЙ У ВЕРТИКАЛЬНІЙ ПЛОЩИНІ, ЗАКРІПЛЕНИЙ ДО СТІНИ

M ≥ T_s

T_s = F ∙ L ∙ sinα (Н∙м)

F = m ∙ g (Н)

- МОМЕНТ ДИНАМІЧНИХ СИЛ (T_f)

Навантаження, на яке впливають зовнішні сили опору руху, такі як сила тертя при переміщенні об'єкту по поверхні. Потребує запас по крутному моменту (3 ÷ 5) ∙ T_f

M = крутний момент циліндра (Н∙м)

μ = коефіцієнт тертя

m = маса об'єкту (кг)

g = прискорення вільного падіння (м/с² )

ЦИЛІНДР ПЕРЕМІЩУЄ ОБ'ЄКТ ПО ПОВЕРХНІ

M ≥ (3 ÷ 5) ∙ T_f (Н∙м)

F = μ ∙ m ∙ g (Н)

g = 9.8 (м ⁄c² )

T_f = F ∙ L (Н∙м)

- РЕЗУЛЬТУЮЧИЙ МОМЕНТ ІНЕРЦІЇ (T_а)

Необхідно розрахувати момент інерції і взяти коефіцієнт запасу, рівний 5 ÷ 10: (5 ÷ 10) ∙ T_а

M = крутний момент циліндра (Н∙м)

l = момент інерції (кг∙м² )

α = кутове прискорення (рад/с² )

θ = кут повороту

t = час повороту (с)

В прикладі єдина сила, яку необхідно подолати – сила інерції. Динамічна і статична сила рівні 0.

ЦИЛІНДР ЗДІЙСНЮЄ ПОВОРОТ ОБ'ЄКТУ БЕЗ ПРОТИДІЇ ЗОВНІШНІХ СИЛ

M ≥ 10 ∙ T_a (Н∙м)

T_a = I ∙ α (Н∙м)

α = (2 ∙ θ)/t² (рад ⁄с² )

Момент інерції обчислюється в залежності від форми переміщуваного об'єкту. На рисунку наведений приклад розрахунку – коли центр мас не співпадає з віссю обертання:

I = K + m ∙ L² - результуючий момент інерції

K = m · a² + b² – момент інерції паралелепіпеда

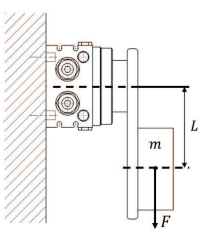
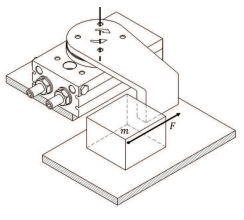
Для наведеного прикладу момент інерції розраховується наступним чином:

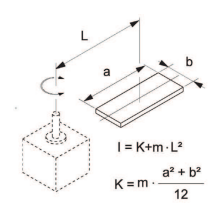
l₁ = момент інерції плити

l₃ = момент інерції об'єкту

Сумарний момент інерції (l):

Розрахуйте кутове прискорення (α). Виходячи з умов: кут повороту θ = 90° = π/2 рад при t = 0.9 с., ви отримаєте:

Таким чином необхідний крутний момент рівний результуючому моменту інерції (Ta) з урахуванням коефіцієнту запасу.

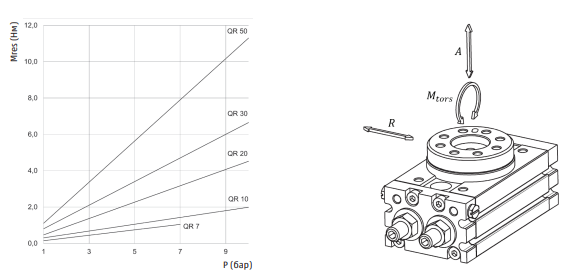
3) МАКСИМАЛЬНО ДОПУСТИМА КІНЕТИЧНА ЕНЕРГІЯ:

Перевірте, чи не перевищує кінетична енергія, що розвиває циліндр, допустимий діапазон значень в розділі «максимально допустима кінетична енергія і час повороту»

Розрахуйте кутову швидкість (ω)

Кінетична енергія (E)

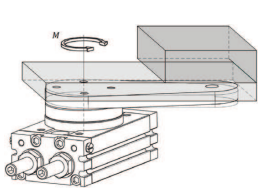
4) МАКСИМАЛЬНО ДОПУСТИМЕ НАВАНТАЖЕННЯ:

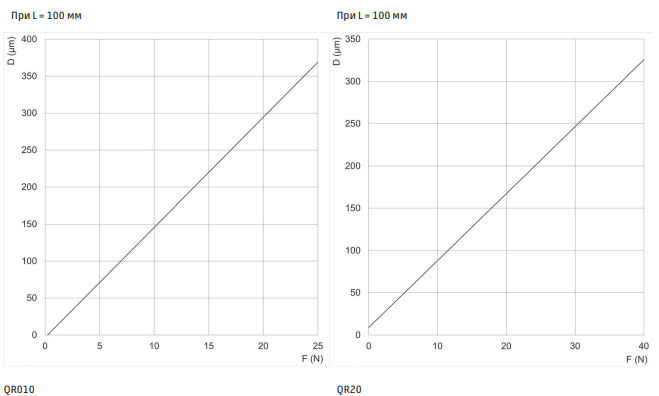
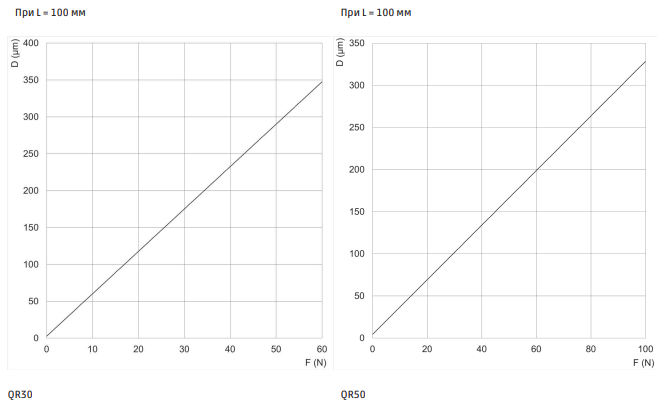
Перевірте, чи не перевищує значення осьової і радіальної сили, а також згинального моменту допустимі значення, представлені в розділі «вихідний крутний момент і допустиме навантаження» і чи задовільняє їх сумарне відношення умові:

W_s = осьове навантаження

A = максимально допустиме осьове навантаження

Wr = радіальне навантаження

R = максимально допустиме радіальне навантаження

M_tors = згинальний момент

M = максимально допустимий згинальний момент

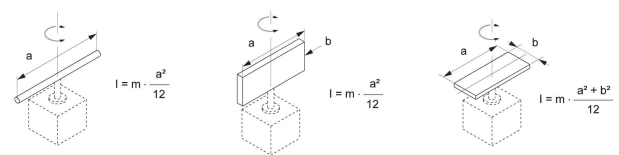
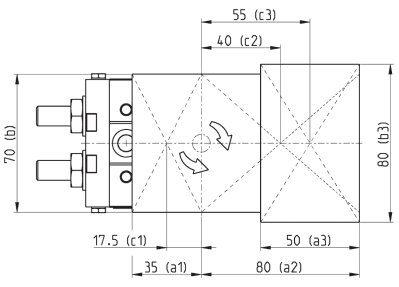
I₁ = m₁ ∙(a₁² + b² ) ⁄ 12 + m₁ ∙c₁² + m₂ ∙(a₂²+b₂ ) ⁄ 12 + m₂ ∙c₂² = 0.5∙(0.0352 + 0.072 )/12 + 0.5 ∙ 0.01752 + 1.5∙(0.082 + 0.072 ) ⁄ 12 + 1.5∙0.0402 = 0.0042 кг∙м²

I₃ =m₃ ∙(a₃² + b₃² ) ⁄ 12 + m₃ ∙ c₃² = 3.0 ∙ (0.052 + 0.082 ) ⁄ 12 + 3.0 ∙ 0.0552 = 0.0109 кг∙м²

I = I₁ + I₃ = 0.0042 + 0.0109 = 0.0151 кг∙м²

α = 2 ∙ θ ⁄ t₂ = (2∙π ⁄2) ⁄ 0.92 = 3.88 рад/с²

10 ∙ T_а = 10 ∙ I ∙ α

10 ∙ T_а = 10 ∙ 0.0151 ∙ 3.88 = 0.58 Н∙м

ω = θ/t = π/2 ∙ t = 3.14/2 ∙ 0.9 = 1.74 рад/с

Ek = (I ∙ ω²)/2 = (0.0151 ∙ 1.74²)/2 = 0.023 Дж

Ws/A + Wr/R + Mtors/M ≤1

ОСЬОВЕ НАВАНТАЖЕННЯ (Ws)

Осьове навантаження розраховується:

РАДІАЛЬНЕ НАВАНТАЖЕННЯ (Wr) – радіальне навантаження відсутнє

ЗГИНАЛЬНИЙ МОМЕНТ (M_tors)

F1 = вага частини плити зліва від центру обертання (Н)

с₁ = плече сили F1 (м)

F₂ = вага частини плити справа від центру обертання (Н)

с₂ = плече сили F2 (м)

Mtors1 = згинальний момент плити

F3 = вага об'єкту

M_tors3 = згинальний момент об'єкту

mт = m₁ + m₂ + m₃ = 0.5 + 1.5 + 3.0 = 5.0 кг

W_s = mт ∙ g = 5.0 ∙ 9.8 = 49 Н

F₁ = m₁ ∙ g = 0.5 ∙ 9.8 = 4.9 Н

F₂ = m₂ ∙ g = 1.5 ∙ 9.8 = 14.7 Н

M_tors1 = -F₁ ∙ c₁ + F₂ ∙ c₂ = -4.9 ∙ 0.0175 + 14.7 ∙ 0.04 = 0.5 Н∙м

F₃ = m₃ ∙ g = 3.0 ∙ 9.8 = 29.4 Н

M_tors3 = F₃ ∙ c₃ = 29.4 ∙ 0.055 = 1.62 Н∙м

M_tors = M_tors1 + M_tors3 = 0.5 + 1.62 = 2.12 Н∙м

Результуючим згинальним моментом є сума двох моментів M_tors1 + Mtors3:

ВИБІР ЦИЛІНДРА:

1. Критерій «Час повороту» 0.9с/90° задовільняють всі розміри.

2. Критерій «Крутний момент» 0.58 Нм при тиску не більше 4 бар гарантують: QR10, QR20, QR30, QR50.

3. Критерій «Максимально допустима кінетична енергія»

0.023 Дж гарантують: QR20, QR30, QR50 – з амортизаторами або без.

QR10S – тільки з амортизаторами.

4. Критерій «Максимально допустиме навантаження» задовільняють: QR20, QR30, QR50.

Результуючим вибором є модель: QR20A з механічним остановом або QR20S з гідроамортизаторами, або модель більшого діаметру.

1 – ВАЛ

Вісь обертання співпадає з віссю центру мас

2 – ПРЯМОКУТНИЙ

ВІсь обертання паралельна стороні b, центр мас співпадає з центром вісі обертання

3 – ПРЯМОКУТНИК І ПАРАЛЕЛЕПІПЕД

Вісь обертання перпендикулярна стороні a, центр мас співпадає з центром вісі обертання

4 – ДИСК

Вісь обертання співпадає з віссю центру мас

5 – СФЕРА

Вісь обертання співпадає з віссю центру мас

6 – ДИСК

Вісь обертання співпадає з віссю центру мас

7 – ЦИЛІНДР

Вісь обертання співпадає з віссю центру мас

8 – Вісь обертання і центр мас не співпадають.

K = момент інерції центру мас (для прикладу обрана фігура 4 – ДИСК)