-
Переміщення
- Пневмоциліндри за міжнародними стандартами
- Компактні пневмоциліндри (притискні)
- Пневмоциліндри з неіржавної сталі
- Пневмоциліндри з вбудованими напрямними
- Пневмоциліндри не за стандартом
- Поворотні пневмоциліндри
- Безштокові пневмоциліндри
- Магнітні датчики положення
- Додаткове приладдя до циліндрів
- Спеціальні рішення
- Управління
- З’єднання
- Підготовка повітря
- Магістральна підготовка повітря
- Трубопровідна арматура
- Захвати Пневматичні
- Компоненти вакуумної системи
- Електричні приводи
Нова продукція
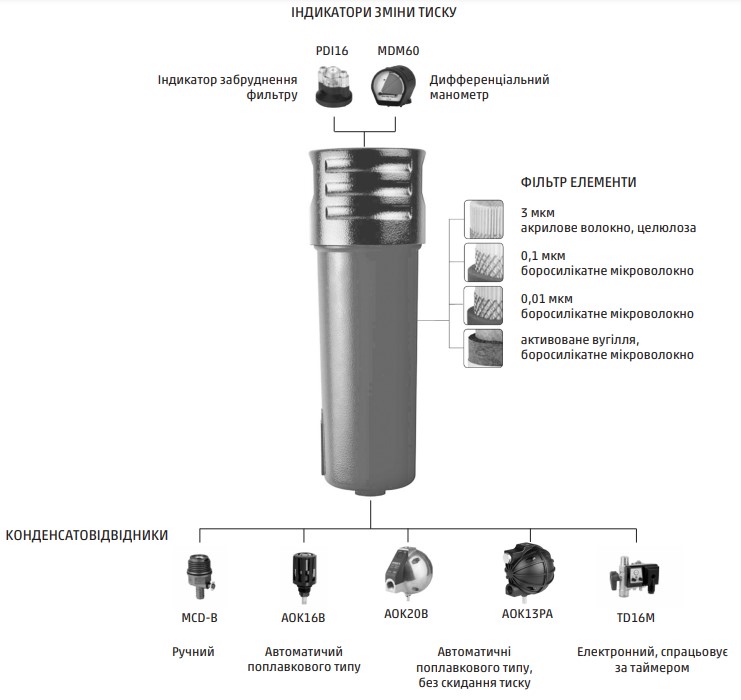
Циклонні сепаратори розроблені для високоефекти
Магістральний фільтр - це спеціальни
Фільтри серії FYD розроблені для високоеф
Фільтри F4-...-О2 для роботи з киснем були спец
Опис
Поворотні циліндри Серії QR з подвійним поршнем здатні забезпечити високий крутний момент при високій стабільності і точному куті повороту. Кут повороту може бути встановлений в діапазоні від 0° до 190° за допомогою регулювальних гвинтів або гідравлічних амортизаторів, розташованих на одній зі сторін столу. Використання амортизаторів дозволяє забезпечувати в два-п'ять разів більше кінетичної енергії, ніж виконання з регулювальними гвинтами. Поворотний стіл компактний і допускає пряме навантаження. Компактність, легкість і простота в поєднанні з профільними промисловими конструкціями роблять ці циліндри особливо підходящими для використання в складальних і пакувальних секторах будь-якого застосування, де потрібне переміщення, нахил або поворот об'єктів.
МАКСИМАЛЬНО ДОПУСТИМА КІНЕТИЧНА ЕНЕРГІЯ І ЧАС ПОВОРОТУ
| Розмір | Максимально допустима кінетична енергія (Дж) | Максимально допустима кінетична енергія (Дж) | Налаштування діапазону часу повороту для стабільного використання (с/90˚) | Налаштування діапазону часу повороту для стабільного використання (с/90˚) |
| З регулювальними гвинтами | З амортизаторами | З регулювальними гвинтами | З амортизаторами | |
| 07 | 0.006 | - | 0.2 - 1.0 | - |
| 10 | 0.01 | 0.04 | 0.2 - 1.0 | 0.2 - 1.0 |
| 20 | 0.025 | 0.12 | 0.2 - 1.0 | 0.2 - 1.0 |
| 30 | 0.05 | 0.12 | 0.2 - 1.0 | 0.2 - 1.0 |
| 50 | 0.08 | 0.30 | 0.2 - 1.0 | 0.2 - 1.0 |
ГЕОМЕТРИЧНІ ДОПУСКИ ПОВОРОТНОГО СТОЛА
 |
P = Допуск паралельності поворотного стола 0,1 мм R = Допуск круглості поворотного стола 0,1 мм C = Допуск циліндричності поворотного стола 0,1 мм |
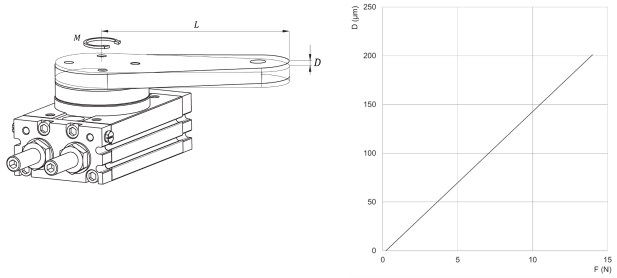
ВІДХИЛЕННЯ ПЛОЩИНИ СТОЛА ВІД ГОРИЗОНТАЛЬНОГО ПОЛОЖЕННЯ
 |
|
|
M = Момент/крутний момент L = Відстань від вісі обертання до крайньої точки D = Відхилення від горизонталі |
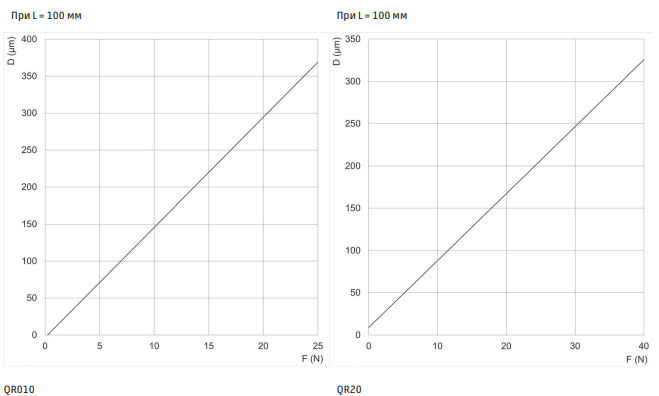
QR07 При L = 100 мм D = Відхилення від горизонталі F = Зусилля |
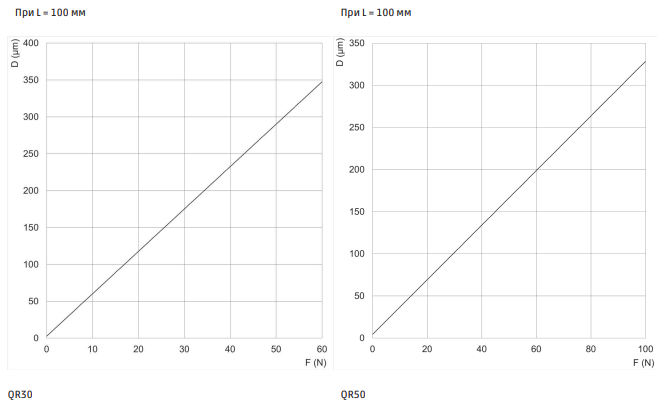
НЕУЗГОДЖЕНІСТЬ ПОВОРОТНОГО СТОЛА
 |
|
|
D = Відхилення від горизонталі F = Зусилля |
D = Відхилення від горизонталі F = Зусилля |
 |
|
|
D = Відхилення від горизонталі F = Зусилля |
D = Відхилення від горизонталі F = Зусилля |
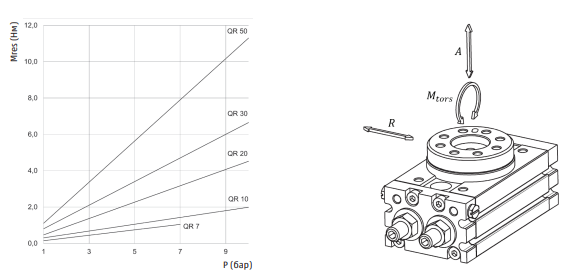
ВИХІДНИЙ КРУТНИЙ МОМЕНТ І ДОПУСТИМІ НАВАНТАЖЕННЯ
 |
|||||||||||||||||||||||||
|
Mres = Крутний момент P = Тиск |
Максимально допустиме навантаження
|
||||||||||||||||||||||||
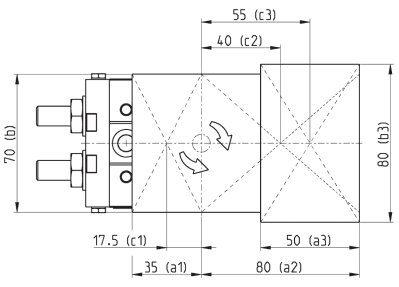
РОЗМІР/ВИБІР ЦИЛІНДРА
ЯК ПРАВИЛЬНО ОБРАТИ ЦИЛІНДР:
ВИХІДНІ ДАНІ:
Тиск: 4 бар (0.4 МПа)
Кут повороту: 90°
Час повороту: 0.9 с
Навантаження:
m1 = маса плити зліва від вісі обертання 0.5 кг
m2 = маса плити справа від вісі обертання 1.5 кг
m3 = маса переміщуваного об'єкту 3.0 кг
1) ЧАС ПОВОРОТУ:
Перевірте, чи задовольняє необхідний час повороту допустимому діапазону значень в розділі «кінетична енергія і час повороту»
Необхідний час повороту: 0.9 с/90°
2) КРУТНИЙ МОМЕНТ:
Перевірте, чи задовольняє необхідний крутний момент допустимому діапазону значень в розділі «крутний момент і допустимі навантаження»
|
МОМЕНТ ПРИКЛАДЕНИХ СИЛ:
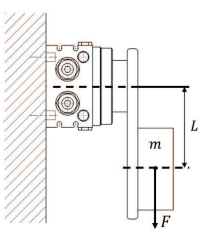
- МОМЕНТ СТАТИЧНИХ СИЛ (Ts) Статична сила циліндра – сила, що виробляється навантаженням при відсутності переміщень. Наприклад, вага об'єкту при негоризонтальному розташуванні площини обертання F = вага переміщуваних мас (Н) L = плече між центром мас і віссю обертання Ts = момент, створюваний силою тяжіння (Н∙м) α = кут відхилення вісі обертання об'єкту від вертикальної вісі
|
ЦИЛІНДР РОЗТАШОВАНИЙ У ВЕРТИКАЛЬНІЙ ПЛОЩИНІ, ЗАКРІПЛЕНИЙ ДО СТІНИ
M ≥ Ts Ts = F ∙ L ∙ sinα (Н∙м) F = m ∙ g (Н) |
|
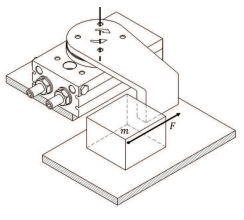
- МОМЕНТ ДИНАМІЧНИХ СИЛ (Tf) Навантаження, на яке впливають зовнішні сили опору руху, такі як сила тертя при переміщенні об'єкту по поверхні. Потребує запас по крутному моменту (3 ÷ 5) ∙ Tf
M = крутний момент циліндра (Н∙м) μ = коефіцієнт тертя m = маса об'єкту (кг) g = прискорення вільного падіння (м/с2 )
|
ЦИЛІНДР ПЕРЕМІЩУЄ ОБ'ЄКТ ПО ПОВЕРХНІ
M ≥ (3 ÷ 5) ∙ Tf (Н∙м) F = μ ∙ m ∙ g (Н) g = 9.8 (м ⁄c2 ) Tf = F ∙ L (Н∙м) |
|
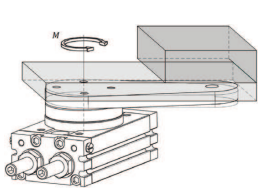
- РЕЗУЛЬТУЮЧИЙ МОМЕНТ ІНЕРЦІЇ (Tа) Необхідно розрахувати момент інерції і взяти коефіцієнт запасу, рівний 5 ÷ 10: (5 ÷ 10) ∙ Tа
M = крутний момент циліндра (Н∙м) l = момент інерції (кг∙м2 ) α = кутове прискорення (рад/с2 ) θ = кут повороту t = час повороту (с) В прикладі єдина сила, яку необхідно подолати – сила інерції. Динамічна і статична сила рівні 0.
|
ЦИЛІНДР ЗДІЙСНЮЄ ПОВОРОТ ОБ'ЄКТУ БЕЗ ПРОТИДІЇ ЗОВНІШНІХ СИЛ
M ≥ 10 ∙ Ta (Н∙м) Ta = I ∙ α (Н∙м) α = (2 ∙ θ)/t2 (рад ⁄с2 )
|
|
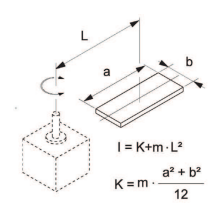
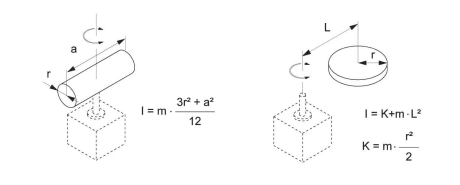
Момент інерції обчислюється в залежності від форми переміщуваного об'єкту. На рисунку наведений приклад розрахунку – коли центр мас не співпадає з віссю обертання: I = K + m ∙ L2 - результуючий момент інерції K = m · a2 + b2 – момент інерції паралелепіпеда |
|
|
Для наведеного прикладу момент інерції розраховується наступним чином: l1 = момент інерції плити l3 = момент інерції об'єкту Сумарний момент інерції (l): Розрахуйте кутове прискорення (α). Виходячи з умов: кут повороту θ = 90° = π/2 рад при t = 0.9 с., ви отримаєте: Таким чином необхідний крутний момент рівний результуючому моменту інерції (Ta) з урахуванням коефіцієнту запасу.
3) МАКСИМАЛЬНО ДОПУСТИМА КІНЕТИЧНА ЕНЕРГІЯ: Перевірте, чи не перевищує кінетична енергія, що розвиває циліндр, допустимий діапазон значень в розділі «максимально допустима кінетична енергія і час повороту»
Розрахуйте кутову швидкість (ω)
Кінетична енергія (E)
4) МАКСИМАЛЬНО ДОПУСТИМЕ НАВАНТАЖЕННЯ: Перевірте, чи не перевищує значення осьової і радіальної сили, а також згинального моменту допустимі значення, представлені в розділі «вихідний крутний момент і допустиме навантаження» і чи задовільняє їх сумарне відношення умові: Ws = осьове навантаження A = максимально допустиме осьове навантаження Wr = радіальне навантаження R = максимально допустиме радіальне навантаження Mtors = згинальний момент M = максимально допустимий згинальний момент |
I1 = m1 ∙(a12 + b2 ) ⁄ 12 + m1 ∙c12 + m2 ∙(a22+b2 ) ⁄ 12 + m2 ∙c22 = 0.5∙(0.0352 + 0.072 )/12 + 0.5 ∙ 0.01752 + 1.5∙(0.082 + 0.072 ) ⁄ 12 + 1.5∙0.0402 = 0.0042 кг∙м2
I3 =m3 ∙(a32 + b32 ) ⁄ 12 + m3 ∙ c32 = 3.0 ∙ (0.052 + 0.082 ) ⁄ 12 + 3.0 ∙ 0.0552 = 0.0109 кг∙м2
I = I1 + I3 = 0.0042 + 0.0109 = 0.0151 кг∙м2 α = 2 ∙ θ ⁄ t2 = (2∙π ⁄2) ⁄ 0.92 = 3.88 рад/с2 10 ∙ Tа = 10 ∙ I ∙ α 10 ∙ Tа = 10 ∙ 0.0151 ∙ 3.88 = 0.58 Н∙м
ω = θ/t = π/2 ∙ t = 3.14/2 ∙ 0.9 = 1.74 рад/с
Ek = (I ∙ ω2)/2 = (0.0151 ∙ 1.742)/2 = 0.023 Дж
Ws/A + Wr/R + Mtors/M ≤1
|
|
ОСЬОВЕ НАВАНТАЖЕННЯ (Ws) Осьове навантаження розраховується: РАДІАЛЬНЕ НАВАНТАЖЕННЯ (Wr) – радіальне навантаження відсутнє ЗГИНАЛЬНИЙ МОМЕНТ (Mtors)
F1 = вага частини плити зліва від центру обертання (Н) с1 = плече сили F1 (м) F2 = вага частини плити справа від центру обертання (Н) с2 = плече сили F2 (м) Mtors1 = згинальний момент плити F3 = вага об'єкту Mtors3 = згинальний момент об'єкту |
mт = m1 + m2 + m3 = 0.5 + 1.5 + 3.0 = 5.0 кг Ws = mт ∙ g = 5.0 ∙ 9.8 = 49 Н F1 = m1 ∙ g = 0.5 ∙ 9.8 = 4.9 Н F2 = m2 ∙ g = 1.5 ∙ 9.8 = 14.7 Н Mtors1 = -F1 ∙ c1 + F2 ∙ c2 = -4.9 ∙ 0.0175 + 14.7 ∙ 0.04 = 0.5 Н∙м F3 = m3 ∙ g = 3.0 ∙ 9.8 = 29.4 Н Mtors3 = F3 ∙ c3 = 29.4 ∙ 0.055 = 1.62 Н∙м Mtors = Mtors1 + Mtors3 = 0.5 + 1.62 = 2.12 Н∙м |
|
Результуючим згинальним моментом є сума двох моментів Mtors1 + Mtors3:
ВИБІР ЦИЛІНДРА: 1. Критерій «Час повороту» 0.9с/90° задовільняють всі розміри. 2. Критерій «Крутний момент» 0.58 Нм при тиску не більше 4 бар гарантують: QR10, QR20, QR30, QR50. 3. Критерій «Максимально допустима кінетична енергія» 0.023 Дж гарантують: QR20, QR30, QR50 – з амортизаторами або без. QR10S – тільки з амортизаторами. 4. Критерій «Максимально допустиме навантаження» задовільняють: QR20, QR30, QR50. Результуючим вибором є модель: QR20A з механічним остановом або QR20S з гідроамортизаторами, або модель більшого діаметру. |
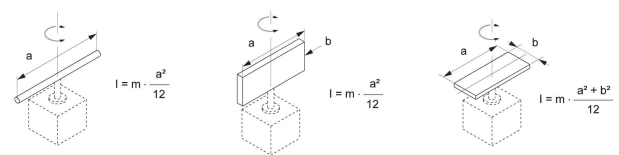
ЯК РОЗРАХУВАТИ МОМЕНТ ІНЕРЦІЇ
 |
||
|
1 – ВАЛ Вісь обертання співпадає з віссю центру мас |
2 – ПРЯМОКУТНИЙ ВІсь обертання паралельна стороні b, центр мас співпадає з центром вісі обертання |
3 – ПРЯМОКУТНИК І ПАРАЛЕЛЕПІПЕД Вісь обертання перпендикулярна стороні a, центр мас співпадає з центром вісі обертання |
 |
||
|
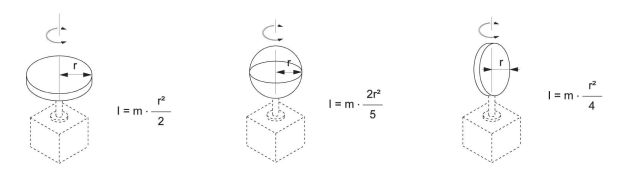
4 – ДИСК Вісь обертання співпадає з віссю центру мас |
5 – СФЕРА Вісь обертання співпадає з віссю центру мас |
6 – ДИСК Вісь обертання співпадає з віссю центру мас |
 |
|
|
7 – ЦИЛІНДР Вісь обертання співпадає з віссю центру мас |
8 – Вісь обертання і центр мас не співпадають. K = момент інерції центру мас (для прикладу обрана фігура 4 – ДИСК) |
Код |
Найменування |
|---|
| Конструкція | рейка-шестерня |
| Дія | двостороння |
| Матеріали |
профіль, кінцеві блоки і поворотний фланець – алюміній; рейка – сталь; шестерня – сталь; ущільнення по корпусу – PTFE; ущільнення – NBR |
| Кріплення | за допомогою гвинтів в центрі |
| Розміри | 7, 10, 20, 30, 50 мм |
| Робоча температура | 0°C ÷ 70°C |
| Стандартний кут повороту | 0° ÷ 190° |
| Мінімальний кут повороту (з амортизатором) | 10 = 66°, 20 = 52°, 30 = 46°, 50 = 70° |
| Повторюваність | < 0,2° |
| Підшипники | кульковий підшипник |
| Робочий тиск | 1 ÷ 10 бар, 1 ÷ 7 бар (для 7 мм), 1 ÷ 6 бар (для версій з амортизатором) |
| Робоче середовище | очищене повітря без необхідності маслорозпилення згідно ISO 8573-1:2010 [7:4:4]. Потребує встановлення відцентрового фільтру 25 мкм, для забезпечення класу очищення повітря за стандартом ISO 8573-1:2010 [7:8:4]. |